Note: Some older web-browsers have trouble rendering inline mathematical characters. If you see question marks or things that look like 'φ' or 'δ' in some of the formulas, that's probably the problem. I couldn't figure out a nice way of making this work everywhere, so you get to suffer :)

That said, this page displays beautifully in Internet Exploder 6, Mozilla 0.9.6, and Opera 6 on both Windows and Macintosh operating systems. If you're not using one of these, perhaps you should.



Table of Contents



Introduction

The number of cases for which Schrödinger's Wave Equation can be solved analytically is very small. However, it is quite common to find that the Hamiltonian for which you wish to solve can be expressed as the sum of a Hamiltonian for which one can solve explicitly and a Hamiltonian for which one can't. If the weight of the unsolvable Hamiltonian is comparatively small, perturbation theory can be used.

In the typical Hamiltonian below, H0 is the Hamiltonian that can be solved explicitly, H' is the Hamiltonian that can't be solved, and λ is a small constant, the perturbation weighting.

(1)

Figure 1: A static Hamiltonian with a time-dependent perturbation
We will investigate the case in which the perturbation potential is time-dependent. This is commonly the case when one is investigating how some system depends upon impinging radiation. The impinging electromagnetic wave causes the electric and magnetic potentials to oscillate, but the oscillations are small compared with the static Hamiltonian. An example of a time-dependent Hamiltonian to which perturbation theory is applicable is in Figure 1. The total Hamiltonian Htot for this system is thus

(2)


Derivation of Time-Dependent Perturbation Theory

If the complete set of solutions to the time-independent Hamiltonian H0 is {Φn} where Φn is an eigenvector with eigenstate En0 (where the zero indicates that this is the energy at t=0), the Schrödinger Equation for the time-independent system in state Φn is

(3)

and the eigenstate Φn at some later time t is given by

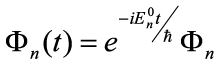.(4)

An arbitrary state Ψ(t) at time t can be specified by a linear combination of eigenstates

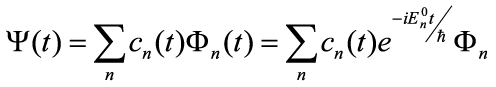(5)

where cn(t) is the probability amplitude of finding the system in state Φn(t) at time t.

We assume that because the perturbed Hamiltonian Htot is very close to the unperturbed Hamiltonian H0, the set of states {Φn(t)} also form a complete set of eigenstates of the perturbed Hamiltonian. Thus, Ψ(t) is also a solution of the perturbed Schrödinger Equation

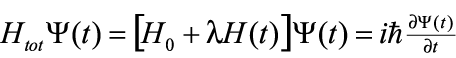.(6)

The main goal of time-perturbation theory is to find the values of the time-dependent probability amplitudes {cn(t)}. This can be accomplished by substituting Eq. (5) into Eq. (6). After a bit of manipulation, this gives

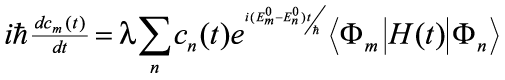.(7)

We can expand cm(t) as an infinite series

.(8)

in which higher order terms become less and less relevant because λ is small. Substituting this series into Eq. (7) and grouping equal-power terms of λ gives the series of equations

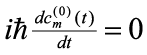(9)

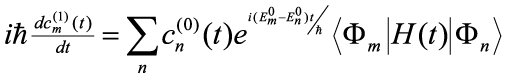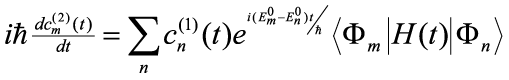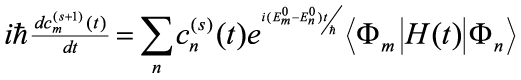This series of equations says that to 0th order, the probability amplitudes are constant; that is, there is no perturbation. We'll examine the 1st order effects on the system. We will assume that at time t=0, the system is in a definite eigenstate Φk so that Ψ(0) = Φk. This implies that cn(0)=δnk. Substituting this into the 1st order equation of Eq. (9) gives

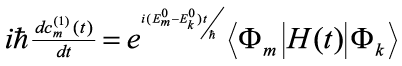.(10)

We can solve this differential equation to find

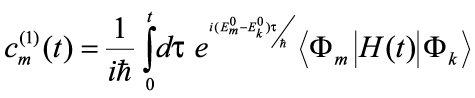.(11)

The term <Φm|H(t)|Φk> is commonly referred to as the 'matrix element' or the 'overlap integral.' It is the probability amplitude that the state formed by operating with the total energy operator H(t) on eigenstate k projects onto state m. We'll denote the matrix element from state k to state m by Hmk. Thus (dropping the notation (1) to indicate that this is a 1st order approximation),

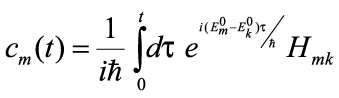.(12)


Fermi's Golden Rule

If we assume that at time t=0, our system is known to be in state i, our initial-time weighting factors are

.(13)

The probability that a system will make a transition from this initial state i to a final state f is then just the probability of finding the system in state f

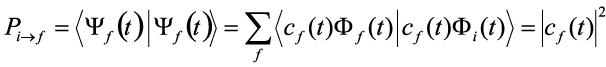.(14)

If our perturbing potential V oscillates periodically with frequency ω and we consider a long time period t, it can be shown that this probability approaches

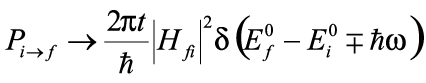.(15)

If we want to find the transition rate Γi→f from initial state i to final state f, we just use the probability per unit time. Thus, the transition rate is

.(16)

This formula is called Fermi's Golden Rule. The δ-function in this formula is an expression of energy conservation. It says that in order to perform the transition, the system must either absorb or emit a quanta of energy ħω from the potential field.


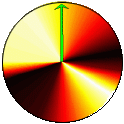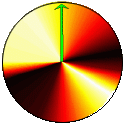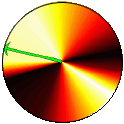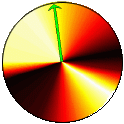Figure 2: Illustration of k-vector transitions in Fermi's Golden Rule
Fermi's Golden Rule gives the probability of a transition from some initial state to some final state. Figure 2 illustrates possible changes to the k-vector for a hypothetical solution to Fermi's Golden Rule in which ħω is zero and both Ef0 and Ei0 are proportional to kf2 and ki2. In the figure, the transition probabilities are represented by a disk of various colors; light-yellow represents states with a high selection probability, while dark-red represents states with a low selection probability. The probabilities form a disk because the magnitude of the final k-vector is equal to the magnitude of the initial k-vector (since ħω=0). The animation shows a series of likely transitions from the initial k-vector based on the transition probabilities. The initial k-vector points straight up. Notice that all of the transitions are from the (given) initial state to final states of high probability.

Figure 2 was generated using a custom MATLAB script. The script uses random numbers to compute the probability disk and then uses a simple Monte Carlo technique to model a series of transitions.



Lifetimes and Linewidths of Excited States

Let's investigate the behavior of a system that makes a transition from one state to another and then relaxes back to the original state. We'll assume an atomic system that consists of a single atom with a single electron. At some time t=0, the electron is excited to a higher energy. At some later time, it relaxes back to the ground state, emitting a photon.

We'll denote the ground state (with the photon included) by φ0(k) and the excited state (without a photon) by φ1(k). We'll only consider the excited state φ1 with energy E (that is, the excited state is momentum-independent). This subset of possible excited states satisfies the eigenequation

.(17)

Correspondingly, the ground state φ0(k) satisfies the eigenequation

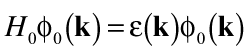.(18)

Thus, the state of the system at any time t (assuming a time-independent Hamiltonian H0) is a superposition of the available states

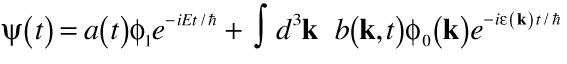.(19)

We'll assume that the coupling potential V between the two states is small, a valid assumption for electromagnetic coupling. The complete system therefore satisfies the eigenequation

.(20)

Using first-order time-dependent perturbation theory as shown above, we can express the scaling coefficient b(k,t) as

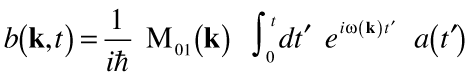(21)

where the matrix element expressing the overlap between the excited and ground states for momentum k is

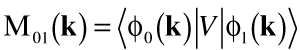(22)

and the energy difference is

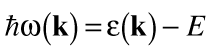.(23)

The postfactor a(t') is a result of the slightly different form of the total state ψ(t).


We can use Fermi's golden rule to show that the decay rate is

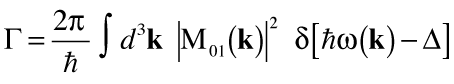(24)

where Δ is the energy necessary for the electron to make a transition between the excited and the ground states.


Let's assume that the probability density of finding the system in the excited state is given by

.(25)

Since the system is known to be in the excited state at time t=0, we also know that a0=1. It can be shown that the assumption for the form of a(t) is correct, and, indeed, that

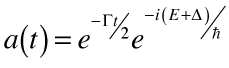.(26)

Thus, the probability of finding the electron in the excited state after a long time t is

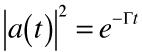.(27)

The probability of finding the electron in the excited state decays exponentially.


Finally, let's examine the probability that the electron is found in ground state φ0(k) at time t=∞. Substituting a(t)=e-zt into the above expression for b(k,t) gives

(28)
,

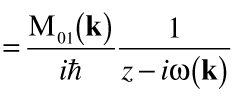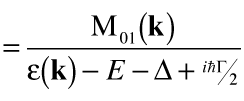so the probability is given by

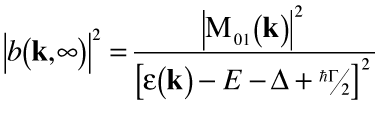.(29)

Since ħΓ is much smaller than the other terms in the denominator, this can be approximated by

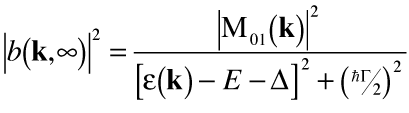.(30)

Thus, the probability of finding the electron in the ground state with momentum k is a Lorentzian centered at the excited energy. As the decay constant Γ increases, the Lorentzian broadens. This is analogous to the spread of a simple Gaussian wavepacket spreading over time.


To restate these conclusions, the probability of finding the electron in the excited state decays exponentially with a time constant equal to the decay rate Γ. The probability of finding the electron in the ground state an arbitrarily long time after measuring it in the excited state is a Lorentzian in k.

Last updated March 17, 2003.
All information herein Copyright ©2000 Jason Harris, All rights reserved.