Note: Some older browsers have trouble rendering the 'hbar' character. If you see question marks in some of the formulas, that's probably the problem. I couldn't figure out a nice way of making this work everywhere, so you get to suffer :)

To begin, lets look at an easy problem involving a rotational Hamiltionian. This is Problem 5, Chapter 11 of Quantum Physics, Second Edition, by Stephen Gasiorowicz.

The Hamiltonian for an axially symmetric rotator is given by

What are the eigenvalues of H?

Solution

For simplicity, lets make the following substitutions

So

Recalling that

we can make the substitution

Using the angular momentum eigenfunctions

We can find the eigenvalues of our Hamiltonian

So, for l=1, we have three energy values E = ħ²(A + C), E = 2ħ²A, and E = ħ²(A + C), corresponding to m = -1, m = 0, and m = 1 respectively.

Alternately, we can express the Hamiltonian in matrix form. When l=1, we can use the matrix operators:

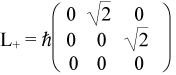
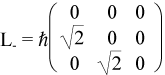
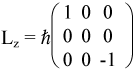
Using the operator relation

we can express L² as

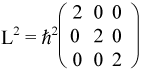
and, by substituting, we can express our Hamiltonian as

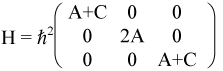
Recalling that we can swap rows and/or columns of a matrix without changing its eigenvalues, lets swap some rows so that we can show the matrix in block-diagonal form.

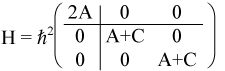
From this representation, it becomes obvious that we have a singlet corresponding to m=0 with energy E = 2Aħ² and a doublet corresponding to m=±1 with energy E = (A + C)ħ².

Now, let's look at something a bit more complicated. This is Problem 5, Chapter 14 of Quantum Physics, Second Edition, by Stephen Gasiorowicz.

You are given the Hamiltonian

Find the eigenvalues of H

• (a) when the angular momentum of the system is 1
• (b) when the angular momentum of the system is 2

Note: The matrix representation of L_x, L_y, L_z for angular momentum 2 are obtainable from

Solution

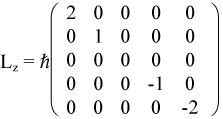
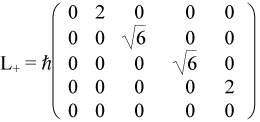
As in the previous problem, we'll make some substitutions to clean up the notation.

So

In order to solve this, we need to be able to express L_x and L_y in terms of L₊ and L_-. So, let's have some fun with operators before we do anything else.

Starting from the definitions of L₊ and L_-

Substituting into the Hamiltonian gives

This can be put into matrix form by replacing the operators with their matrix representations. See this simple MATLAB script to see how. This gives the Hamiltonian in matrix form as

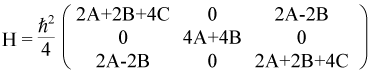
The diagonal corresponds to the solutions for m = -1, 0, 1. As before, we can swap rows and columns to get the matrix in block diagonal form. This corresponds to m = 0, -1, 1.

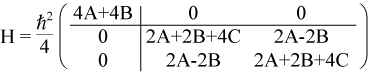
The upper-left block, corresponding to m=0, is equivalent to a singlet with energy ħ²(A+B). The bottom-right block is equivalent to a perturbed Hamiltonian.

Notice that the diagonal terms are sums of the Hamiltonian's coefficients, while the off-diagonal terms are differences. This is consistent with the view that the diagonal terms represent an unperturbed Hamiltonian while the off-diagonal terms represent perturbation. In fact, if the Hamiltonian is represented in this manner, i.e., H = H₀ ± H', the matrix representation would be

So, for this problem, the energy for m = ±1 is

or

Notice that if I₁ = I₂ then A = B and we get the same results we got for the previous problem.

When l=2, the idea is the same, but the matrices are larger. Using the attached MATLAB script, one can obtain the Hamiltonian

Likewise, swapping rows and columns gives us a Hamiltonian in block-diagonal form.

The interpretation is not as obvious as in the above example, but one can see that there are three sets of energies present. There is a singlet with energy E = ħ²(3A+3B) corresponding to m = 0. This was located in the center of the original matrix and can be found within the center of the bottom-right block-diagonal matrices.

There is a doublet of degenerate energies in the top-left corner of the block-diagonal matrix. These have energies of

or

corresponding to m = ±1.

Finally, there is a second doublet in the bottom-right corner of the block-diagonal matrix. This doublet has energies of

or

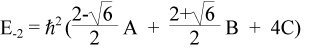
corresponding to m = ±2.

It is interesting to notice what happens if we set A = B in this case. Obviously, we get a diagonal matrix. But physically, setting A = B implies that two of the three Cartesian axes have the same moment of inertia. This situation is physically equivalent to that of a quadrupole in a non-uniform field. To visualize a quadrupole, imagine either an American football or two frisbees placed back to back. Into this shape, insert two negative charges clustered in the center and a positive charge in each tip. Diagram 1 shows a 2-D projection of a quadrupole.

Notice that if one were to place the quadrupole in a uniform external electric field and rotate it along any axis, its potential energy would not change because the torques induced by the two component dipoles would cancel. Conversely, a single dipole would have extremas in potential energy when it was oriented along the direction of the field). If, however, we placed our quadrupole into a non-uniform electric field, the quadrupole would orient itself along the gradient of the field and would have extremas of potential energy when oriented in this direction.

In this situation, the quadrupole can be rotated around one of its axes without changing its potential energy. Rotation around either of the other two axes will cause a change in the potential energy. In other words, the quadrupole has one axis that's invariant to rotation and two that are not.

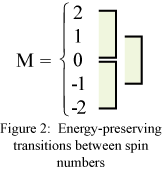Likewise, if A = B, there is one transition of |m| that will not change the energy and two that will (see Figure 2). A transition from m=0 to m=±1 or from m=±1 to m=±2 will change the energy, while a transition from m=0 to m=±2 will not.

This can be explained simply by noting that the m=0 and the m=±2 values reside in the same block-diagonal matrix. Since a diagonal matrix is invariant to certain types of rotations, it makes sense that the matrix containing m=0 and m=±2 keeps the same eigenvalues (energy) when rotated. Also, since these matrices are in block-diagonal form, the matrix that represents transitions of m=±1 is not coupled with that of m=±2, in the same way that rotation of the quadrupole around the energy-invariant axis is not coupled with rotation around the energy-dependent axes.

So physically, the Hamiltonian for angular momentum 2 resembles rotation of a quadrupole in an external non-uniform field. To quote Professor Venables, examples would include the crystal structures taken up by quadrupolar molecules, and the excitations possible in such environments. Quadrupolar radiation is also behind the search for gravitational waves, such as the huge LIGO detectors currently being commissioned in Washington State and Louisiana. In addition there are many electron L=2 examples. For instance, electron d-states in a cubic crystal have exactly this type of splitting, due to crystal field effects. Similarly, the d-states which are implicated in superconductivity in the Cu-O planes of oxide superconductors are thought to involve just one of these subsets (the d-z^2 states) of the Cu d-electrons.