People involved: Jason Harris (undergraduate student, supported via NSF REU Supplement, Award No. ECS-98750S1-001).
As part of this award, A 2D Monte Carlo Particle-based simulator for modeling GaAs devices was developed (this project was partially funded by ONR in the fall semester of 1999). In the theoretical model, all relevant scattering mechanisms for this material (intravalley acoustic and polar optical phonon scattering, and intervalley scattering between the three conduction band valleys D, L and X) were included. We considered both parabolic and non-parabolic analytical bandstructure models. The code was written entirely in ISO C++ and should be portable across all computer architectures. It was tested on computers running x86 Debian Linux, Windows NT and MacOS.
The structure of this code provides a great degree of the simulator's flexibility and distinguishes it from similar device simulators. This was achieved using strict object-oriented philosophy to separate interface from implementation. In addition, reference-counted 'smart' pointers are used extensively for automated trash collection and to simplify both memory management and code legibility. These smart pointers are similar to the autoptr type in the C++ specification, but they handle polymorphism better and are generally more advanced. The simulation software uses recursively encapsulated scattering tables, allowing a reduction in memory requirements and/or processing speed when simulating devices with complicated doping profiles.
In addition, a great deal of flexibility is gained by a newly developed Mesh object used to store and manipulate information about the spatial structure of the device. It converts the positional representation of the device into a mesh of node points used to update the electrostatic potential and local electric field via the solution of Poisson's equation. The Mesh object is also used to modify carriers' scattering tables as they move from one doping region to another. The Mesh object abstracts the device parameters and boundary conditions at each node point into MeshRegions. These MeshRegions are spatial volumes in which the material parameters and boundary conditions remain constant. For example, they can represent heterostructure layers, doping regions, ohmic contacts, or artificial boundaries. Finally, region sizes can be specified using node counts, actual distances, or a combination of node counts and symbolic notation describing the current edges of the device. The combination of this flexibility and the generality of the code implementing the MeshRegions makes describing devices to the simulator quite simple.
Currently, Jason Harris is pursuing a Masters of Science Degree at Arizona State University. His research interests are now directed towards understanding the role of quantum effects in future ultra-small devices.
Simulation results:
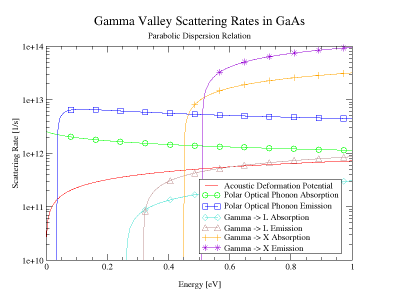
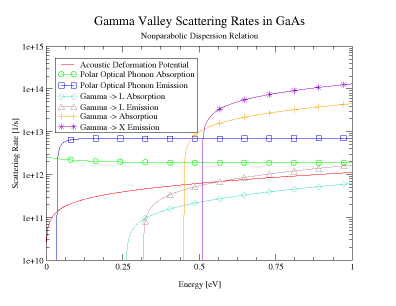
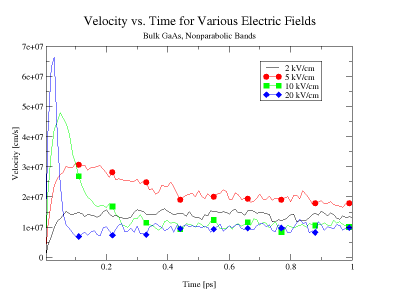
In Figure 13 we show the gamma-valley scattering rates for bulk GaAs material, for both parabolic and non-parabolic energy-wavevector dispersion relation. Comparing the results shown in Figure 13(a) and 13(b), it is obvious that the use of non-parabolic band-structure gives larger values for the scattering rates, due to the increase in the number of final states to which the carriers can scatter. This trend is most pronounced in the case of polar optical phonon scattering. For energies larger than 0.1 eV, the polar optical phonon scattering rate decreases with energy when using parabolic band-structure, and is energy independent when using the non-parabolic band model. In Figure 14(left panel), we show the time-evolution of the average electron drift velocity for the case when a uniform electric field is suddenly applied to the system at time t = 0. For fields smaller than 3 kV/cm, no velocity overshoot is observed. For electric fields larger than 5 kV/cm, there is pronounced velocity overshoot effect, due to the transfer of carriers to the upper-lying valleys. The steady-state velocity-field characteristics of bulk GaAs material are shown on the right panel of Figure 14. The negative differential conductivity is due to the transfer of electrons from the gamma-valley, where they have small effective mass, to the L and X valleys, where they have large effective mass. |
 |
Figure 13. Scattering rates for GaAs. The left pane shown scattering rates using a parabolic dispersion relation, while the right pane shows scattering rates using a nonparabolic dispersion relation.
 |
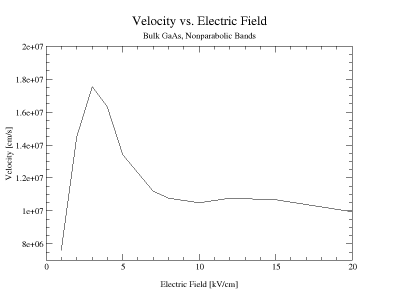 |
Figure 14. (a) Carrier drift velocity evolution for several electric fields. Notice the velocity overshoot that arises because of the difference between the energy relaxation time and the momentum relaxation time. (b) Carrier drift velocity as a function of the electric field.
Presentations: